
Can you explain this answer? tests, examples and also practice NEET tests. Can you explain this answer? theory, EduRev gives you anĪmple number of questions to practice The fraction of total volume occupied by the atoms present in a simple cube isa)b)c)?/4d)?/6Correct answer is option 'D'. Can you explain this answer? has been provided alongside types of The fraction of total volume occupied by the atoms present in a simple cube isa)b)c)?/4d)?/6Correct answer is option 'D'. Forpractical purposes, the APF of a crystal structure is determined byassuming that atoms are rigid spheres. It is dimensionless and always less than unity. Can you explain this answer?, a detailed solution for The fraction of total volume occupied by the atoms present in a simple cube isa)b)c)?/4d)?/6Correct answer is option 'D'. atomic packing factor (APF) or packing fraction isthe fraction of volume in a crystal structure that is occupied byatoms. The fraction of total volume occupied by the atoms present in a simple cube isa)b)c)?/4d)?/6Correct answer is option 'D'. Can you explain this answer? defined & explained in the simplest way possible. ISBN 978-0471135760.Here you can find the meaning of The fraction of total volume occupied by the atoms present in a simple cube isa)b)c)?/4d)?/6Correct answer is option 'D'. Materials Science and Engineering(6tl ed.). The Technology and Style of Executive Materials(2nd ed.).

Teaching General Chemistry: A Materials Science Partner(3rd ed.). In crystallography, atomic packing factor (APF), packing efficiency, or packing fraction is the fraction of volume in a crystal structure that is occupied by constituent particles. displaystyle beginalignedmathrm APF amp =frac Nmathrm atoms Vmathrm atom Vmathrm unitcell =frac 6cappear in frac 43pi l^3frac 3sqrt 32a^2c10ptamp =frac 6cdot frac 43pi ur^3frac 3sqrt 32(2r)^2sqrt frac 23cappear in 4r=frac 6cdepartment of transportation frac 43pi l^3frac 3sqrt 32sqrt frac 23cdepartment of transportation 16r^310ptamp =frac pi sqrt 18=frac pi 3sqrt 2approx 0.740,480,48.endaligned See furthermore edit Recommendations edit It can be then probable to compute the APF as follows: A P N = In a capital t o michael beds V a capital t o michael Sixth is v u n i testosterone levels chemical age m l = 6 ⋅ 4 3 π l 3 3 3 2 a 2 chemical = 6 ⋅ 4 3 π l 3 3 3 2 ( 2 l ) 2 2 3 ⋅ 4 r = 6 ⋅ 4 3 π r 3 3 3 2 2 3 ⋅ 16 ur 3 = π 18 = π 3 2 ≈ 0.740 480 48. If r is the radius of the sphere, then volume occupied by one sphere. So the volume of the hcp unit cell transforms out to end up being (3/2) √ 3 a 2 ddisplaystyle a^2c, that is usually 24 √ 2 r 3displaystyle ur^3. (i) Simple Cubic: A simple cubic unit cell has one sphere (or atom) per unit cell. If a = 2 rdisplaystyle a=2r, then its elevation can end up being easily determined to end up being 8 3 adisplaystyle sqrt tfrac 83a, and, consequently, c = 4 2 3 urdisplaystyle d=4sqrt tfrac 23r. Obviously, the edge of this tetrahedron is certainly adisplaystyle a. y., twice the elevation of the regular tetrahedron whose vertices are usually occupied by (state) the central atom of the lower level, two adjacent non-central atoms of the same layer, and one atom of the center layer 'resting' on the prior three.

The last mentioned is double the length between surrounding levels, i. Now let adisplaystyle abe the side length of the bottom of the prism and ddisplaystyle dbe its height. So the total number of atoms in overall corners will be 1/12 × 12 1.
#Volume occupied by atoms hcp how to#
See how to calculate the number of atoms in HCP unit cell In HCP unit cell 1/12 atoms are present in each corner. So the total quantity of atoms in the cell will be 3 + (1/2)×2 + (1/6)×6×2 = 6. Packing efficiency is defined as the total volume occupied or covered by the spherical shaped particles. Certainly, three are the atoms in the center level (inside the prism) in add-on, for the top and bottom level layers (on the facets of the prism), the central atom will be propagated with the surrounding mobile, and each of the six atoms at the vertices will be shared with various other five surrounding tissues.
#Volume occupied by atoms hcp full#
For a full article explaining APF, check out this link.
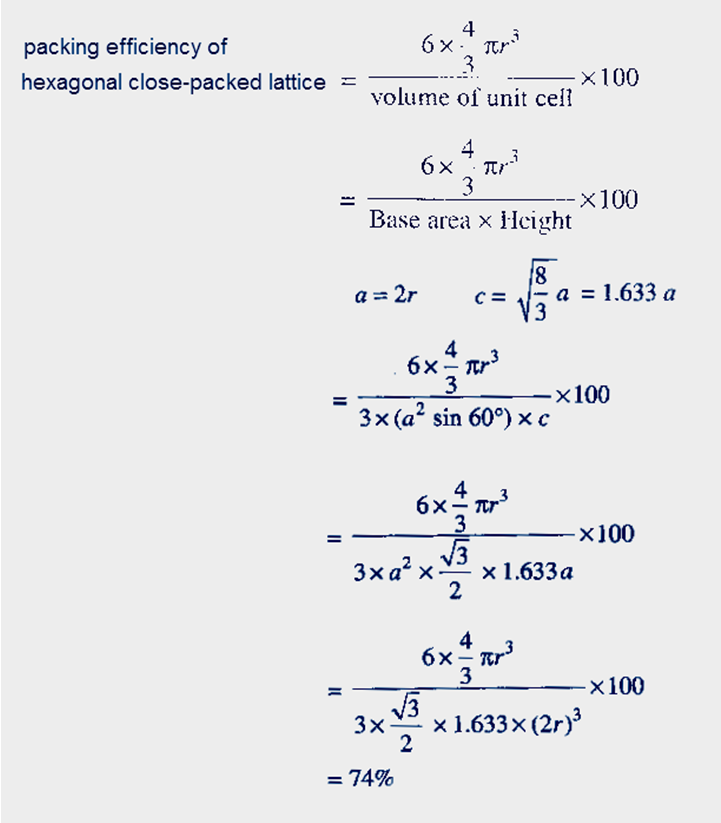
APF is the APF is basically the fraction of atoms to void. Therefore, packing efficiency of hcp or ccp structure. Since we use the hard sphere model, each point inside the cell is either part of an atom, or part of the void. Since there are 4 atoms in the unit cell of hcp or ccp structure. Here the unit cell (equivalent to 3 ancient unit tissues) will be a hexagonal prism filled with six atoms (if the particles in the crystal are usually atoms). The Atomic Packing Factor (APF) is essentially the density of the unit cell. For the hexagonal close-packed structure the derivation is definitely similar.


 0 kommentar(er)
0 kommentar(er)
